r271-635

計算結果の検算

国立天文台の「こよみの計算」で計算した時刻を用いて、次の2つの計算結果を検算する。

（１）光学伏角 θ （真空中の場合の幾何学的解法） + Ephemの空気屈折補正機能

（３）空気屈折伏角（実効値） θref

国立天文台の「こよみの計算」で計算した時刻

国立天文台の「こよみの計算」で手動入力して計算した結果を、コピペした一覧表

年月日,緯度,経度
標高,日の出時刻,日の入り時刻
標高,日の出時刻,日の入り時刻
...


大阪

2025/1/1, 34.67, 135.5
0,07:05,16:58
500,07:01,17:02
1000,06:59,17:04
1500,06:58,17:06
2000,06:56,17:07
2500,06:55,17:08
3000,06:54,17:09
3500,06:54,17:10

2025/7/1, 34.67, 135.5
0,04:48,19:15
500,04:44,19:20
1000,04:42,19:21
1500,04:41,19:23
2000,04:40,19:24
2500,04:39,19:25
3000,04:38,19:26
3500,04:37,19:27


東京

2025/1/1,35.66,139.74
0,06:51,16:39
500,06:46,16:43
1000,06:44,16:45
1500,06:43,16:46
2000,06:42,16:47
2500,06:41,16:48
3000,06:40,16:49
3500,06:39,16:50

2025/7/1,35.66,139.74
0,04:29,19:01
500,04:24,19:05
1000,04:22,19:07
1500,04:21,19:09
2000,04:20,19:10
2500,04:19,19:11
3000,04:18,19:12
3500,04:17,19:13


札幌

2025/1/1,43.07,141.35
0,07:06,16:10
500,07:01,16:15
1000,06:59,16:17
1500,06:57,16:19
2000,06:56,16:20
2500,06:55,16:22
3000,06:54,16:23
3500,06:53,16:24

検証用のPythonスクリプト

日の出・日の入時刻を計算するPythonスクリプト

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

"""指定された緯度・経度・標高に基づき日出・日没時刻を検証するスクリプト。

スクリプト単純実装のテスト用

"""
from datetime import datetime, timedelta
import math
import ephem

target_ymd = "2025/1/1"
R = 6371000.0           # 地球半径 [m]
lat_deg = 34.67         # 緯度
lon_deg = 135.50        # 経度
height_m = 3000         # 標高
refraction_factor = 1.4902      # dip_ref = refraction_factor * dip_geom


def calc_dipgeom_ephemrefraction() -> None:

    pressure_0m = 1013.25   # 標高 0mの気圧 [hPa]
    pressure = pressure_0m * (1 - 2.25577e-5 * height_m) ** 5.2559
    temperature_0m = 15.0   # 標高 0mの気温 [℃]
    temperature = temperature_0m - 0.6 * height_m / 100

    jst_offset = timedelta(hours=9)     # JST → UTC

    # 光学伏角（真空中）
    dip_geom = math.sqrt(2 * height_m / R) * 180.0 / math.pi

    obs = ephem.Observer()
    obs.date = datetime.strptime(target_ymd, "%Y/%m/%d") - jst_offset
    obs.lat = str(lat_deg)
    obs.lon = str(lon_deg)
    obs.elevation = float(height_m)
    obs.pressure = pressure
    obs.temperature = temperature
    obs.horizon = f"-{dip_geom}"

    sun = ephem.Sun()  # type: ignore[reportAttributeAccessIssue]

    # 日の出・日の入り（UTC → JST）
    sunrise = obs.next_rising(sun).datetime() + jst_offset
    sunset = obs.next_setting(sun).datetime() + jst_offset

    print(f"日の出 : {sunrise.strftime('%H:%M:%S')}\n"
          f"日の入 : {sunset.strftime('%H:%M:%S')}\n"
          f"標高 : {height_m} m\n"
          f"補正気圧 : {pressure:5.1f} hPa\n"
          f"補正気温 : {temperature:3.1f} 度\n"
          f"伏角 : {dip_geom:4.3f} °")


def calc_dipref() -> None:

    pressure = 0.0          # Ephemでの空気屈折計算を無効化
    # temperature = 11.0      # Ephemのデフォルト値

    jst_offset = timedelta(hours=9)     # JST → UTC

    # 光学伏角（真空中）
    dip_geom = math.sqrt(2 * height_m / R) * 180.0 / math.pi
    # 実効伏角
    dip_ref = refraction_factor * dip_geom

    obs = ephem.Observer()
    obs.date = datetime.strptime(target_ymd, "%Y/%m/%d") - jst_offset
    obs.lat = str(lat_deg)
    obs.lon = str(lon_deg)
    obs.elevation = float(height_m)
    obs.pressure = pressure
    obs.horizon = f"-{dip_ref}"

    sun = ephem.Sun()  # type: ignore[reportAttributeAccessIssue]

    # 日の出・日の入り（UTC → JST）
    sunrise = obs.next_rising(sun).datetime() + jst_offset
    sunset = obs.next_setting(sun).datetime() + jst_offset

    print(f"日の出 : {sunrise.strftime('%H:%M:%S')}\n"
          f"日の入 : {sunset.strftime('%H:%M:%S')}\n"
          f"標高 : {height_m} m\n"
          f"補正気圧 : {obs.pressure:5.1f} hPa\n"
          f"補正気温 : {obs.temperature:3.1f} 度\n"
          f"伏角 : {dip_ref:4.3f} °")


print("=== 光学伏角 + Ephem空気屈折補正 ===")
calc_dipgeom_ephemrefraction()
print("=== 空気屈折伏角 ===")
calc_dipref()

実行結果で検証

大阪 2025/01/01 標高3000m

=== 光学伏角 + Ephem空気屈折補正 ===
日の出 : 06:53:21
日の入 : 17:09:45
標高 : 3000 m
補正気圧 : 701.1 hPa
補正気温 : -3.0 度
伏角 : 1.758 °
=== 空気屈折伏角 ===
日の出 : 06:53:54
日の入 : 17:09:12
標高 : 3000 m
補正気圧 :   0.0 hPa
補正気温 : 15.0 度
伏角 : 2.620 °

グラフで検証

作成したスクリプトはこのページに掲載するには大きすぎるため、別ファイルとして保存しているPythonスクリプトをダウンロード できる。

赤線が（１）光学伏角 θ （真空中の場合の幾何学的解法） + Ephemの空気屈折補正機能
青線が（３）空気屈折伏角（実効値） θref
黒点が 国立天文台 「こよみの計算」

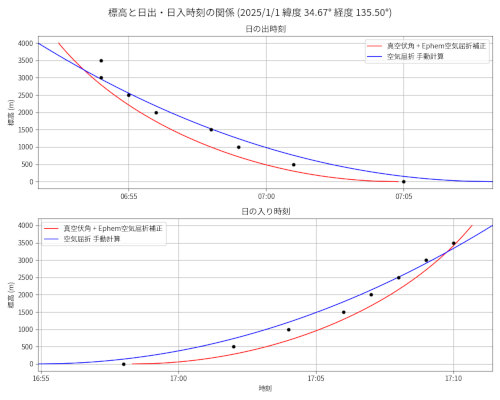
大阪 2025/01/01

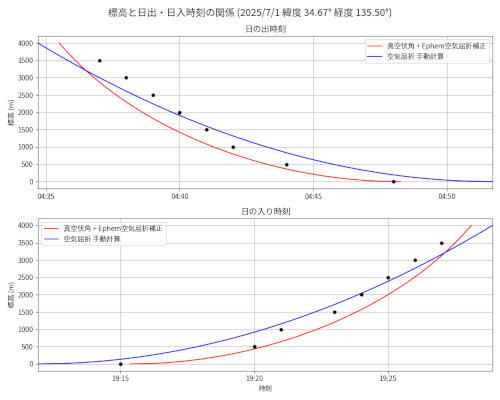
大阪 2025/07/01

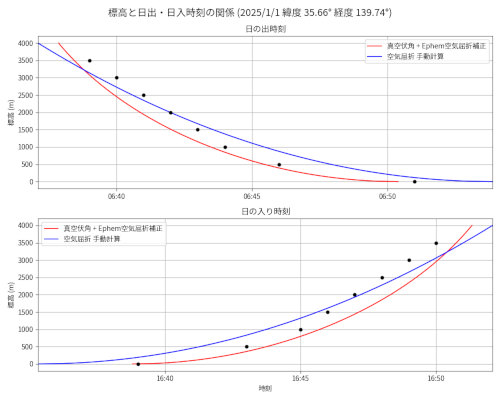
東京 2025/01/01

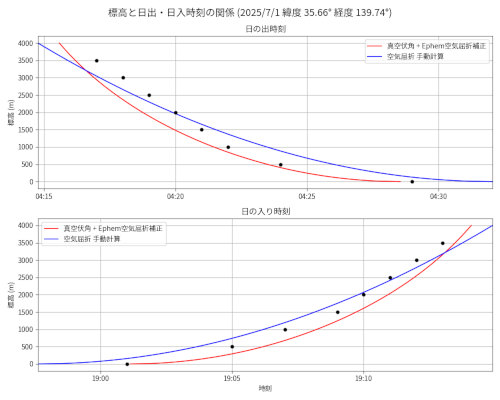
東京 2025/07/01

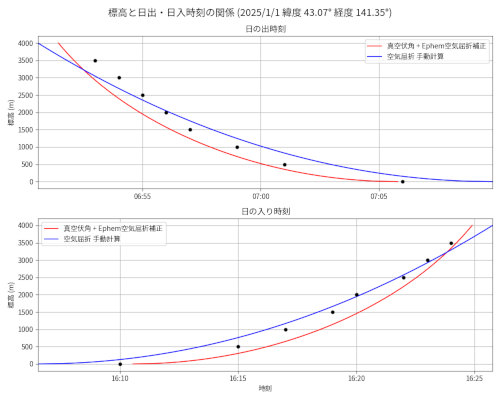
札幌 2025/01/01

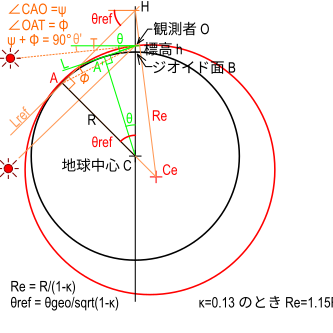
空気屈折率を一定とした場合の実効伏角θrefの幾何学的解法

空気中での光の経路が屈折することにより、見かけ上の水平線より下に実効的な水平線を想定することで得られる伏角を求める。

黒の円周 : 地球のジオイド面で半径はR
赤の円周 : 観測者の場所 O を通り空気屈折し水平線 A まで達するの光の経路を両側に延長した仮想円
C : 地球の中心
Ce : 仮想円の中心
B : 観測者の場所をジオイド面に落とした点
O : 観測者の場所で、ジオイド面から 高さ h の点
A : 観測者が見る水平線上の地点（地球のジオイド面:黒 と仮想円:赤 が接する点）
OT : 観測者 O から見た見かけ上の水平線（オレンジ点線）
θ' : 観測者 O から見た見かけ上の水平線の伏角
ATH : 空気屈折を考慮した水平線地点での黒・赤円の接線 Lref（オレンジ実線）
OA' : 観測者 O から見た真空時の水平線（緑の実線）
θ : 観測者 O から見た真空時の伏角

観測者から見かけ上の水平線までの距離 : AOの長さ

地球中心と観測者・水平線を結んだ三角形CAOについて余弦定理を用いて関係を表す

θrefが極めて小さい場合

と近似できるため

H << R を考慮すると

∠OAT ( = Φ ) を伏角 θref で表す

地球中心と観測者・水平線を結んだ三角形CAOについて正弦定理を用いて関係を表す

θrefが極めて小さい場合、また R >> h の場合、次の近似ができる。

Φが小さい場合は 次のように近似できるため

(11)と(12)を合わせると

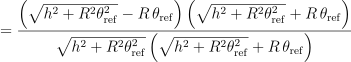
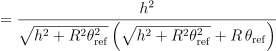
分母に対してRθrefをそれぞれ外に出すと

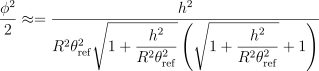
ここで、次行に示すテイラー展開の公式の第2項までを用いることにする

のようにすれば

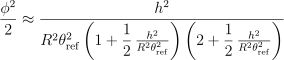
ここで と置いて

分数部分の一部は次のように表記できる

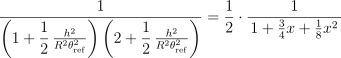
ここで再びテイラー展開の公式（第2項まで） において次行のように置けば

次のように表記できる

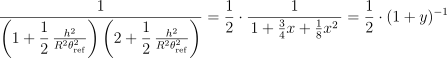
xの1次までにまるめて（x^2 以上は切り捨てして）

ここからもとの式に戻していく

ここでテイラー展開 で第2項までの近似を用いてルートを外すと

ここで、 を用いて、Φを消すと

θref^3を掛けて、すべての項を左辺側に移すと

ここでθref^2 = x と置き、κ/2 = b, h/R = a と置くと

さらに b = A, -a = B, 3/8 a^3 = C と置くと、

二次方程式の解の公式により

x, a, b に戻すと

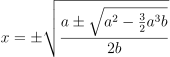
ここで、a = h/R がかなり小さな値であることを考慮すると のように近似できるため

解の次元（光学伏角はhの1/2乗で、空気屈折伏角がhの1/4乗）というのはおかしく、さらにいえば屈折率が上がれば伏角が（1/κの1/4乗に比例して）小さくなるは理屈に合わない。つまり、ちゃんと問題が解けていないのだ。

私の実力では、解は得られなかった...