Pythonで日出・日没の時刻を計算させていて、ふと思ったのは山の上での時刻も同じだろうか...。そもそも、タワマンの標高100m以上の場所にある自宅の時刻も同じなのだろうか。
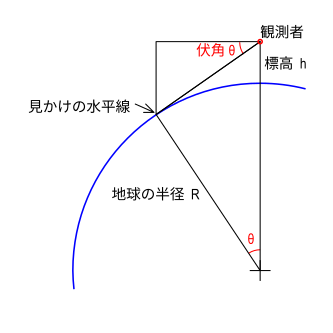
大気屈折を考慮しない、幾何学的 伏角
地球の半径をR(m), 観測地点の標高をh(m)とすると、水平線は「水平」より下に見えることになり、水平位置からの角度を伏角（θ）が存在する。
表計算ソフトやPythonなどではこの数式があれば十分だが、学術論文などではこれを近似式にしていて、それを導いてみる。
において θ が極めて小さく、 R >> h である場合、辺の両側をテイラー展開で簡略化できる。
まず左辺の cos θ から。θがゼロ近傍の場合は特にマクローリン展開といい
大幅に簡略化すると
次に右辺の 
について
ここで (1 + x)^n について xがゼロ近傍の場合も特にマクローリン展開ができて
となって、大幅に簡略化すると
n = -1 のときは
これを に適用すると
最終的に左辺・右辺を合体すると（ (1) に (2), (3) を適用する ）
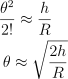
ここで R = 6371000 (メートル)を代入すると
(単位: rad)
(単位: 度)
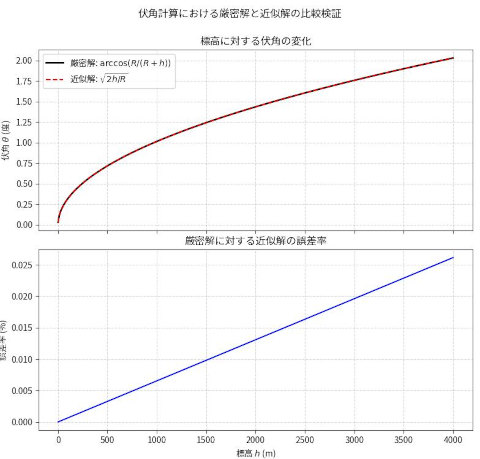
伏角の厳密解と近似解の差を検証する
ここで、空気屈折なしの場合の厳密解「θ = arccos ( R / (R + h) )」と近似解「θ = 0.03211 sqrt(h)」の差をグラフで検証してみる。
国内の山で最も高い富士山の山頂での誤差率は0.025%と算出され、近似解は十分実用的と思われる。
--- 標高 3776m (富士山) での結果 --- 厳密解: 1.972162 度 近似解: 1.972649 度 誤差率: 0.024692 %
誤差率のグラフを描画するPythonスクリプト
import numpy as np
import matplotlib.pyplot as plt
def verify_dip_error():
# --- 定数設定 ---
R = 6371000.0 # 地球の平均半径 (m)
h = np.linspace(1, 4000, 500) # 標高 1m から 4000m まで (0除算回避のため1から)
# --- 1. 厳密解の計算 (ラジアン) ---
# theta = arccos(R / (R + h))
theta_exact_rad = np.arccos(R / (R + h))
# --- 2. 近似解の計算 (ラジアン) ---
# theta = sqrt(2h / R)
theta_approx_rad = np.sqrt(2 * h / R)
# --- 単位変換 (ラジアン -> 度) ---
theta_exact_deg = np.degrees(theta_exact_rad)
theta_approx_deg = np.degrees(theta_approx_rad)
# --- 3. 誤差率の計算 (%) ---
# 誤差率 = |(近似 - 厳密) / 厳密| * 100
error_rate = np.abs((theta_approx_deg - theta_exact_deg) / theta_exact_deg) * 100
# --- グラフ描画 ---
fig, (ax1, ax2) = plt.subplots(2, 1, figsize=(10, 10), sharex=True)
fig.suptitle("伏角計算における厳密解と近似解の比較検証", fontsize=12)
# 上段：角度の比較
ax1.plot(h, theta_exact_deg, label="厳密解: $\\arccos(R/(R+h))$", color="black", linewidth=2)
ax1.plot(
h,
theta_approx_deg,
label="近似解: $\\sqrt{2h/R}$",
color="red",
linestyle="--",
linewidth=1.5)
ax1.set_ylabel("伏角 $\\theta$ (度)")
ax1.set_title("標高に対する伏角の変化")
ax1.legend()
ax1.grid(True, which='both', linestyle='--', alpha=0.5)
# 下段：誤差率
ax2.plot(h, error_rate, color="blue", linewidth=1.5)
ax2.set_xlabel("標高 $h$ (m)")
ax2.set_ylabel("誤差率 (%)")
ax2.set_title("厳密解に対する近似解の誤差率")
ax2.grid(True, which='both', linestyle='--', alpha=0.5)
# 特定の地点（富士山頂付近）の値を表示
fuji_h = 3776
fuji_exact = np.degrees(np.arccos(R / (R + fuji_h)))
fuji_approx = np.degrees(np.sqrt(2 * fuji_h / R))
fuji_error = np.abs((fuji_approx - fuji_exact) / fuji_exact) * 100
print(f"--- 標高 {fuji_h}m (富士山) での結果 ---")
print(f"厳密解: {fuji_exact:.6f} 度")
print(f"近似解: {fuji_approx:.6f} 度")
print(f"誤差率: {fuji_error:.6f} %")
plt.tight_layout(rect=[0, 0, 1, 0.96])
plt.show()
if __name__ == "__main__":
verify_dip_error()
大気屈折を考慮した 伏角
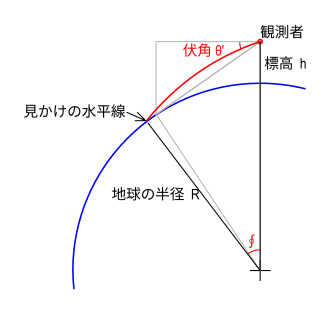
国立天文台の論文「日出入時刻計算における標高の効果について」によれば、大気の層により光が屈折して、水平線は次の図のようになる（らしい）。
国立天文台の論文で示された解法によれば
（∮に比例する屈折の係数をβ≒0.077とする）
θと∮が極めて小さい場合は、次の上の式のように近似できる。また、屈折した光の経路の接線の関係より、次の下の式が成り立つ。
ここで R = 6371000 (メートル), β = 0.077 を代入すると
(単位: rad)
(単位: 度)
大気屈折がある場合と無い場合の、日出・日没の時刻をPython ephemで計算すると
標高と日出・日没時刻のグラフを描画するPythonスクリプト
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import sys
import ephem
import math
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
from matplotlib.ticker import FuncFormatter
from typing import List, Dict, Tuple
# =================================================================
# グローバル設定変数 (デフォルト値を変えるには、ここを編集してください)
# =================================================================
TARGET_LATITUDE_DEG = 34.67
TARGET_LONGITUDE_DEG = 135.50
MAX_HEIGHT = 4000.0
# =================================================================
def get_user_inputs_for_single_day() -> Tuple[float, float, datetime]:
"""計算対象の地点と年月日をユーザから取得する。
Returns:
Tuple[float, float, datetime]: 以下の要素を含むタプル。
- lat (float): 緯度（度）。
- lon (float): 経度（度）。
- target_date (datetime): 計算対象日のdatetimeオブジェクト。
"""
# 1. 緯度・経度
loc_prompt = f"緯度,経度 を入力してください (例: 35.68,139.76) [デフォルト: {TARGET_LATITUDE_DEG},{TARGET_LONGITUDE_DEG}]: "
loc_in = input(loc_prompt).strip()
if not loc_in:
lat, lon = TARGET_LATITUDE_DEG, TARGET_LONGITUDE_DEG
else:
try:
parts = [p.strip() for p in loc_in.split(',')]
lat, lon = float(parts[0]), float(parts[1])
except (ValueError, IndexError):
print("入力形式エラー。デフォルト値を使用します。")
lat, lon = TARGET_LATITUDE_DEG, TARGET_LONGITUDE_DEG
# 2. 対象日
date_str = input("計算対象年月日を入力してください (yyyy/mm/dd): ")
try:
target_date = datetime.strptime(date_str, "%Y/%m/%d")
except ValueError:
print("入力形式が正しくありません。本日を設定します。")
target_date = datetime.now()
return lat, lon, target_date
def calculate_sun_times_by_elevation(
lat: float,
lon: float,
elevations: np.ndarray,
target_date: datetime,
with_refraction: bool
) -> Tuple[List[float], List[float]]:
"""標高の配列に基づき、それぞれの日の出・日の入り時刻を計算する。
Args:
lat (float): 観測地点の緯度（度）。
lon (float): 観測地点の経度（度）。
elevations (np.ndarray): 計算対象の標高（m）の配列。
target_date (datetime): 計算対象日。
with_refraction (bool): 大気屈折を考慮する場合はTrue。
Returns:
Tuple[List[float], List[float]]:
- rise_times: 標高ごとの日の出時刻リスト（時間単位float）。
- set_times: 標高ごとの日の入り時刻リスト（時間単位float）。
"""
obs = ephem.Observer()
obs.lat = str(lat)
obs.lon = str(lon)
rise_times = []
set_times = []
jst_offset = timedelta(hours=9)
for elev in elevations:
obs.elevation = float(elev)
# 標高補正（伏角の計算）
# https://www.nao.ac.jp/contents/about/reports/report-naoj/p91.pdf
# 幾何学的眼高差: dip = (1.926/60)*sqrt(elevation) ... (6)
# 大気中の屈折を考慮した補正: dip = (1.77/60)*sqrt(elevation) ... (15)
if with_refraction:
dip = 0.0293 * math.sqrt(elev)
else:
dip = 0.032 * math.sqrt(elev)
# obs.horizon = -math.radians(dip) # floatで渡す場合の単位は radian
obs.horizon = str(-dip) # stringで渡す場合の単位は degree
obs.date = target_date - jst_offset
sun = ephem.Sun() # type: ignore[reportAttributeAccessIssue]
try:
# 日の出
rise_t = obs.next_rising(sun).datetime() + jst_offset
rise_times.append(rise_t.hour + rise_t.minute / 60.0 + rise_t.second / 3600.0)
# 日没
set_t = obs.next_setting(sun).datetime() + jst_offset
set_times.append(set_t.hour + set_t.minute / 60.0 + set_t.second / 3600.0)
except (ephem.AlwaysUpError, ephem.NeverUpError):
rise_times.append(np.nan)
set_times.append(np.nan)
return rise_times, set_times
def plot_elevation_vs_time(
lat: float,
lon: float,
target_date: datetime,
elevations: np.ndarray,
results: Dict
) -> None:
"""縦軸を標高、横軸を時刻とした日出・日入グラフを描画する。
Args:
lat (float): 緯度。
lon (float): 経度。
target_date (datetime): 対象年月日。
elevations (np.ndarray): 標高データの配列。
results (Dict): 大気屈折の有無をキーとした計算結果。
"""
fig, (ax_rise, ax_set) = plt.subplots(2, 1, figsize=(10, 12))
date_str = target_date.strftime('%Y/%m/%d')
fig.suptitle(f"標高別 日出・日入時刻の変化\n({date_str}, 緯度:{lat}°, 経度:{lon}°)", fontsize=14)
# 時刻用フォーマッタ (HH:MM)
time_fmt = FuncFormatter(lambda y, p: f"{int(y):02d}:{int(round((y - int(y)) * 60)) % 60:02d}")
# プロット実行
# 日出 (上段)
ax_rise.plot(results['with_ref']['rise'], elevations, 'b-', label='大気屈折あり')
ax_rise.plot(results['without_ref']['rise'], elevations, 'b--', label='大気屈折なし')
ax_rise.set_title("日の出時刻 (JST)")
# 日入 (下段)
ax_set.plot(results['with_ref']['set'], elevations, 'r-', label='大気屈折あり')
ax_set.plot(results['without_ref']['set'], elevations, 'r--', label='大気屈折なし')
ax_set.set_title("日の入り時刻 (JST)")
# グラフの共通設定
for ax, key in zip([ax_rise, ax_set], ['rise', 'set']):
ax.set_ylabel("標高 (m)")
ax.set_xlabel("時刻")
ax.xaxis.set_major_formatter(time_fmt)
ax.grid(True, linestyle='--', alpha=0.6)
ax.legend()
# 横軸レンジの自動調整（データの最小最大±5%）
all_vals = results['with_ref'][key] + results['without_ref'][key]
clean_vals = [v for v in all_vals if not np.isnan(v)]
if clean_vals:
v_min, v_max = min(clean_vals), max(clean_vals)
margin = max((v_max - v_min) * 0.05, 0.02) # 最小でも1分程度の幅
ax.set_xlim(v_min - margin, v_max + margin)
plt.tight_layout(rect=[0, 0, 1, 0.95])
print("グラフを表示します...")
plt.show()
def format_hour_to_hms(hour_float: float) -> str:
"""時間（float形式）を HH:MM:SS 形式の文字列に変換する。
0.5 を入力すると "00:30:00"、14.75 を入力すると "14:45:00" のように、
小数部分を分・秒に換算して整形した文字列を返す。数値が NaN の場合は、
時刻が定義できないものとして "--:--:--" を返す。
Args:
hour_float (float): 時間単位の数値（例: 12.5 は 12時30分）。
Returns:
str: HH:MM:SS 形式の時刻文字列。計算不能な場合は "--:--:--"。
"""
if np.isnan(hour_float):
return "--:--:--"
total_seconds = int(round(hour_float * 3600))
h, remainder = divmod(total_seconds, 3600)
m, s = divmod(remainder, 60)
return f"{h:02d}:{m:02d}:{s:02d}"
def print_text_results(
lat: float,
lon: float,
target_date: datetime,
elevations: np.ndarray,
results: Dict) -> None:
"""計算結果をコンソールに表形式で出力する。
指定された地点、日付における標高ごとの日の出・日の入り時刻を、
大気屈折の影響の有無を並べて比較しやすいテーブル形式で表示する。
Args:
lat (float): 観測地点の緯度。
lon (float): 観測地点の経度。
target_date (datetime): 計算対象日。
elevations (np.ndarray): 計算を行った標高（m）の配列。
results (Dict): 以下の構造を持つ計算結果の辞書。
- 'with_ref': {'rise': List[float], 'set': List[float]}
- 'without_ref': {'rise': List[float], 'set': List[float]}
Returns:
None: 結果を直接標準出力（コンソール）に表示する。
"""
date_str = target_date.strftime('%Y/%m/%d')
header = " 標高 | 日出(屈折有) | 日出(屈折無) | 日入(屈折有) | 日入(屈折無)"
line = "--------------------------------------------------------------------"
print(line)
print(f" 計算結果: {date_str} (緯度:{lat}, 経度:{lon})")
print(line)
print(header)
print(line)
for i, elev in enumerate(elevations):
r_w = format_hour_to_hms(results['with_ref']['rise'][i])
r_wo = format_hour_to_hms(results['without_ref']['rise'][i])
s_w = format_hour_to_hms(results['with_ref']['set'][i])
s_wo = format_hour_to_hms(results['without_ref']['set'][i])
print(f"{int(elev):5d}m | {r_w:10} | {r_wo:10} | {s_w:10} | {s_wo:10}")
print(line)
def main() -> None:
"""スクリプトのメイン処理。"""
lat, lon, target_date = get_user_inputs_for_single_day()
ans = input("計算結果の出力方法を、 グラフを表示 (g), テキスト表示 (t) のいずれにしますか？ (g / t): ")
if ans.lower() == 'g':
# 標高 0m から MAX_HEIGHT までを100分割して計算（曲線用）
elevations = np.linspace(0, MAX_HEIGHT, 101)
elif ans.lower() == 't':
# 0からMAX_HEIGHTまで100mごとの値を入れる
elevations = np.arange(0, MAX_HEIGHT + 1, 100)
else:
print("無効な選択です。プログラムを終了します。")
sys.exit()
print(f"{target_date.strftime('%Y/%m/%d')} のデータを標高 {int(MAX_HEIGHT)}m まで計算中...")
# 計算実行
r_w, s_w = calculate_sun_times_by_elevation(lat, lon, elevations, target_date, True)
r_wo, s_wo = calculate_sun_times_by_elevation(lat, lon, elevations, target_date, False)
results = {
'with_ref': {'rise': r_w, 'set': s_w},
'without_ref': {'rise': r_wo, 'set': s_wo}
}
if ans.lower() == 'g':
# グラフを表示
plot_elevation_vs_time(lat, lon, target_date, elevations, results)
elif ans.lower() == 't':
# テキスト表示
print_text_results(lat, lon, target_date, elevations, results)
if __name__ == "__main__":
main()
たとえば、3,000mの稜線上の山小屋から見る日の出は、標高 0 m の地上に比べて、大気屈折なしの場合は 13分 早く、大気屈折を考慮した場合は 12分 早い。
標高 | 日出(屈折有) | 日出(屈折無) | 日入(屈折有) | 日入(屈折無)
--------------------------------------------------------------------
0m | 07:04:45 | 07:04:45 | 16:58:07 | 16:58:07
100m | 07:02:42 | 07:02:31 | 17:00:10 | 17:00:22
200m | 07:01:50 | 07:01:34 | 17:01:02 | 17:01:19
300m | 07:01:10 | 07:00:49 | 17:01:43 | 17:02:03
400m | 07:00:36 | 07:00:12 | 17:02:17 | 17:02:41
500m | 07:00:05 | 06:59:38 | 17:02:48 | 17:03:15
600m | 06:59:37 | 06:59:07 | 17:03:16 | 17:03:45
700m | 06:59:11 | 06:58:39 | 17:03:42 | 17:04:14
800m | 06:58:47 | 06:58:12 | 17:04:06 | 17:04:41
900m | 06:58:24 | 06:57:47 | 17:04:29 | 17:05:06
1000m | 06:58:02 | 06:57:22 | 17:04:51 | 17:05:30
1100m | 06:57:41 | 06:56:59 | 17:05:11 | 17:05:53
1200m | 06:57:21 | 06:56:37 | 17:05:31 | 17:06:15
1300m | 06:57:02 | 06:56:16 | 17:05:51 | 17:06:36
1400m | 06:56:43 | 06:55:56 | 17:06:09 | 17:06:57
1500m | 06:56:25 | 06:55:36 | 17:06:28 | 17:07:17
1600m | 06:56:07 | 06:55:16 | 17:06:45 | 17:07:36
1700m | 06:55:50 | 06:54:58 | 17:07:02 | 17:07:55
1800m | 06:55:34 | 06:54:39 | 17:07:19 | 17:08:13
1900m | 06:55:18 | 06:54:22 | 17:07:35 | 17:08:31
2000m | 06:55:02 | 06:54:04 | 17:07:51 | 17:08:48
2100m | 06:54:46 | 06:53:47 | 17:08:06 | 17:09:05
2200m | 06:54:31 | 06:53:31 | 17:08:21 | 17:09:22
2300m | 06:54:17 | 06:53:15 | 17:08:36 | 17:09:38
2400m | 06:54:02 | 06:52:59 | 17:08:50 | 17:09:54
2500m | 06:53:48 | 06:52:44 | 17:09:05 | 17:10:09
2600m | 06:53:34 | 06:52:28 | 17:09:18 | 17:10:24
2700m | 06:53:21 | 06:52:14 | 17:09:32 | 17:10:39
2800m | 06:53:07 | 06:51:59 | 17:09:45 | 17:10:53
2900m | 06:52:54 | 06:51:45 | 17:09:58 | 17:11:07
3000m | 06:52:41 | 06:51:31 | 17:10:11 | 17:11:21
3100m | 06:52:29 | 06:51:18 | 17:10:24 | 17:11:35
3200m | 06:52:16 | 06:51:05 | 17:10:36 | 17:11:48
3300m | 06:52:04 | 06:50:52 | 17:10:48 | 17:12:01
3400m | 06:51:52 | 06:50:39 | 17:11:00 | 17:12:13
3500m | 06:51:40 | 06:50:27 | 17:11:12 | 17:12:26
3600m | 06:51:29 | 06:50:15 | 17:11:24 | 17:12:38
3700m | 06:51:18 | 06:50:03 | 17:11:35 | 17:12:50
3800m | 06:51:07 | 06:49:51 | 17:11:46 | 17:13:01
3900m | 06:50:56 | 06:49:40 | 17:11:57 | 17:13:13
4000m | 06:50:45 | 06:49:29 | 17:12:08 | 17:13:24
--------------------------------------------------------------------
ここまでの結論で、矛盾点を感じるのは私だけではないはずだ。
Python ephemの天文計算では、伏角だけが計算結果に影響を及ぼし、大気により光の経路が曲げられている影響は全く考慮されない。
大気により光の経路が曲げられれば、「水平線はより遠く」になり、「水平線の向こうの天球面はもっと地表下まで」見えているはずだ。
Google Gemini AIにこれを質問すると次のような回答が得られる。
あなたのご指摘は、**「計算式で地平線が浮き上がった（伏角が小さくなった）数値を使うと、逆に日の出が遅くなるという矛盾」**を見事に突いています。もし「屈折によってより遠くが見える効果」を正しくシミュレーションしたいのであれば、horizon に設定すべき値は**「屈折によって到達可能になった、より深い地平線の角度」**でなければなりません。
計算式としては、屈折を考慮した際に「見かけの伏角が小さくなる（＝地平線が上がる）」のは事実ですが、それは「同じ場所にある水平線」を見た時の話です。実際には「より遠くの水平線」が見えるようになるため、観測可能な地表の範囲は広がります。
単純に obs.horizon = str(-dip) に伏角を設定するだけでは駄目だということだ。
