天体望遠鏡で撮影するとき、アイピースを使って眼視する場合の視野角を計算してみる
Excelの自動計算シート
20230307_viewangle_calc.xlsxをダウンロードする
撮像素子(CCD・CMOS等)の場合の視野角計算
回答
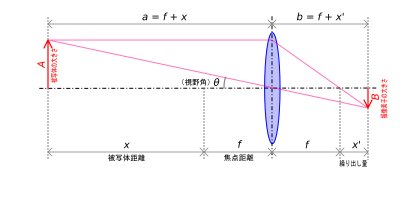
撮像素子の寸法 2*B
望遠鏡の焦点距離 f
視野角 2*θ = 2*B / f (rad) = 2*B / f * 360 / 2Π (度)
-----
撮像素子寸法 2*B = (mm)
焦点距離 f = (mm)
数学的証明
tanθ = B / (f+x')
θ = atan( B / (f+x') ) ...①
ここで、ガウスの公式
1/a + 1/b = 1/f
1/(f+x) + 1/(f+x') = 1/f ...②
x → ∞ のとき、 1/(f+x) → 0となるため
②は、 1/(f+x') = 1/f となり、 x' = 0 といえる
したがって①は
θ = atan( B/f ) ...③
逆三角関数 atan のテイラー展開(マクローリン展開)は
atan θ = θ - θ^3/3 + θ^5/5 - θ^7/7 + ...
ここで、無限遠方の場合は θ≒0 であるため第2項以下はゼロとして
atan θ = θ
したがって③は次のように簡略化される
θ = B / f
アイピースで眼視の場合の視野角計算
回答
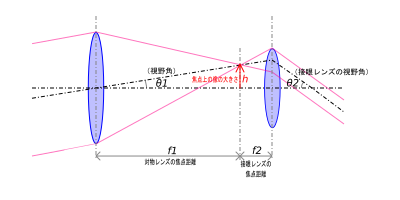
望遠鏡の焦点距離 f1
アイピースの焦点距離 f2
アイピースの視野角 2*θ2
倍率 M = f1 / f2
視野角 2*θ1 = 2*θ2 / M
-----
望遠鏡の焦点距離 f1 = (mm)
アイピースの焦点距離 f2 = (mm)
アイピースの視野角 2*θ2 = (度)
数学的証明
tanθ1 = h / f1
tanθ2 = h / f2 ... ①
ここで、三角関数のテイラー展開(マクローリン展開)は
sinθ = θ/1! - θ^3/3! + θ^5/5! - θ^7/7! + ....
cosθ = 1 - θ^2/2! + θ^4/4! - θ-6/6! + ...
ここで、無限遠方の場合は θ≒0 であるため第2項以下はゼロとして
sinθ = θ
cosθ = 1
tanθ = sinθ / cosθ = θ
したがって、①は次のように近似される
θ1 = h / f1
θ2 = h / f2
θ1*f1 = h
θ2*f2 = h
θ1*f1 = θ2*f2 ... ②
ここで、倍率 M は、視野角の比であるため
M = θ2/θ1
よって、②はこのMを用いて
M = θ2/θ1 = f1/f2
θ1 = θ2 / M = θ2 / (f1/f2)